-
Définition des saisons
-
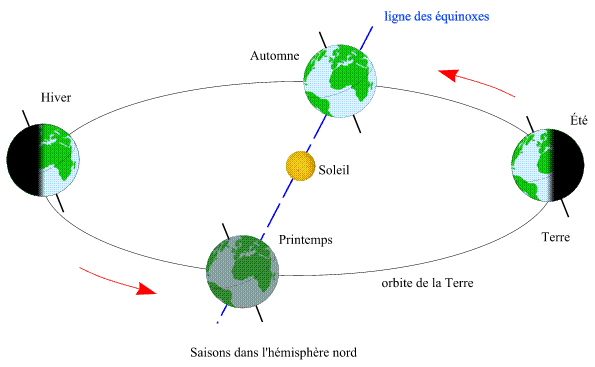
L'orbite de la Terre autour du Soleil
-
La rotation de la Terre et l'équateur terrestre
-
La ligne des équinoxes et la ligne des
solstices
-
La durée des jours et des nuits
-
Les dates des saisons
-
La révolution tropique
-
Pourquoi les saisons tombent-elles toujours aux
mêmes dates ?
-
Les calendriers utilisés dans le programme
de calcul
-
La dérive des saisons dans le calendrier
julien
-
Les dates des saisons dans le calendrier grégorien
-
La durée des différentes saisons
-
La longueur des saisons
-
L'évolution de la longueur des saisons
-
Un peu d'histoire
-
La précession des équinoxes et la
longueur de l'année tropique
-
La longueur des saisons
1. Définition des saisons
1.1. L'orbite de la Terre autour du Soleil
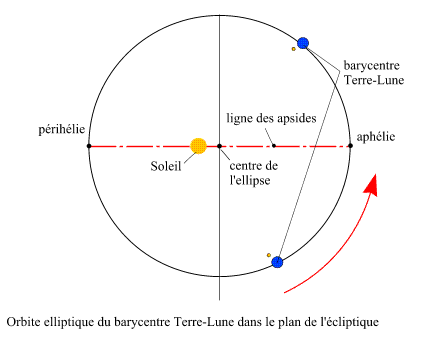
En première approximation, le barycentre du système Terre-Lune
parcourt, dans le sens direct (sens inverse des aiguilles d'une montre),
une orbite quasi elliptique et plane autour du Soleil (première
loi de Kepler). Le plan de cette orbite est appelé plan de l'écliptique.
Le Soleil est situé à l'un des foyers de cette ellipse. L'excentricité
de l'ellipse est tellement faible qu'elle est indécelable sur le
tracé de l'orbite, le tracé ressemble à celui d'un
cercle. Il est important de noter que le Soleil ne se trouve pas au centre
de l'ellipse mais à l'un de ces foyers. La distance entre le barycentre
Terre-Lune et le Soleil n'est donc pas constante. Il y a deux positions
particulières correspondant aux valeurs extrêmes de cette
distance : le périhélie (distance minimale) et l'aphélie
(distance maximale). La ligne joignant ces deux positions s'appelle ligne
des apsides.
1.2. La rotation de la Terre et l'équateur terrestre
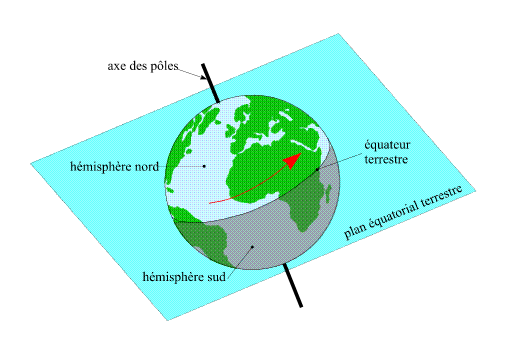
La Terre tourne sur elle-même, autour de l'axe des pôles, dans
le sens direct (d'ouest en est). L'axe de rotation de la Terre n'est pas
normal au plan de l'orbite du barycentre Terre-Lune (plan de l'écliptique).
Cette inclinaison, de 23° 26', est à l'origine des variations
de la durée des jours et des nuits ainsi que des saisons. Le plan
normal à l'axe de rotation terrestre coupant en deux hémisphères
la sphère terrestre s'appelle plan équatorial terrestre.
L'intersection de ce plan avec la Terre est l'équateur terrestre.
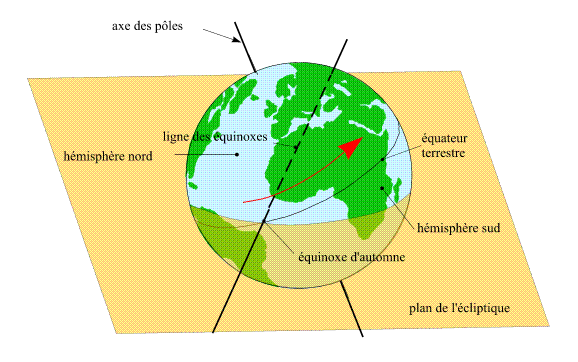
1.3. La ligne des équinoxes et la ligne des solstices
Comme l'axe de rotation de la Terre n'est pas normal au plan de l'écliptique,
le plan équatorial terrestre n'est pas parallèle au plan
de l'écliptique. Il le coupe donc suivant une droite. Cette droite
s'appelle la ligne des équinoxes. Lorsque la direction du segment
joignant le Soleil à la Terre est parallèle à cette
ligne, la Terre se trouve aux équinoxes.
Il existe une autre ligne particulière, la ligne perpendiculaire,
dans le plan de l'écliptique, à la ligne des équinoxes.
Cette ligne est la ligne des solstices. Lorsque la direction du segment
joignant le Soleil à la Terre est parallèle à cette
ligne, la Terre se trouve aux solstices.
Vu de la Terre, dans le repère équatorial géocentrique,
l'équinoxe correspondant au passage du Soleil des déclinaisons
négatives aux déclinaisons positives est appelé équinoxe
de printemps (début du printemps dans l'hémisphère
nord) ou point vernal. Cette direction est, dans le plan de l'écliptique,
l'origine des longitudes célestes et elle est également,
dans le plan de l'équateur, l'origine des ascensions droites.
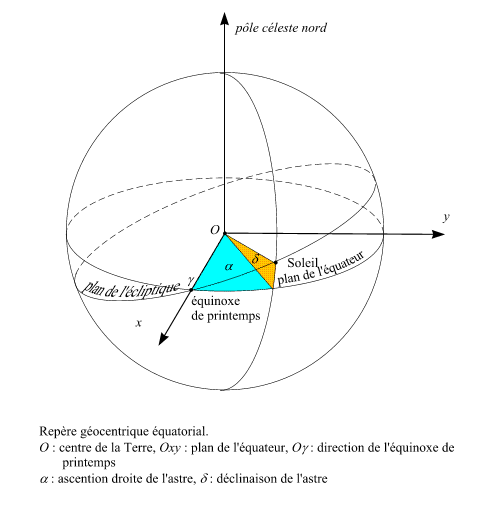
Le printemps, dans l'hémisphère nord, correspond donc
à l'instant où la longitude géocentrique apparente
du centre du Soleil est égale à 0°. L'autre équinoxe,
correspondant au passage du Soleil des déclinaisons positives aux
déclinaisons négatives, est appelé équinoxe
d'automne (début de l'automne dans l'hémisphère nord).
L'automne, dans l'hémisphère nord, correspond donc à
l'instant où la longitude géocentrique apparente du centre
du Soleil est égale à 180°.
Le solstice situé entre l'équinoxe de printemps et l'équinoxe
d'automne est le solstice d'été et le solstice compris entre
l'équinoxe d'automne et l'équinoxe de printemps est le solstice
d'hiver. L'été, dans l'hémisphère nord, correspond
donc à l'instant où la longitude géocentrique apparente
du centre du Soleil est égale à 90°. De même, le
solstice d'hiver, dans l'hémisphère nord, correspond à
l'instant où la longitude géocentrique apparente du centre
du Soleil est égale à 270°.
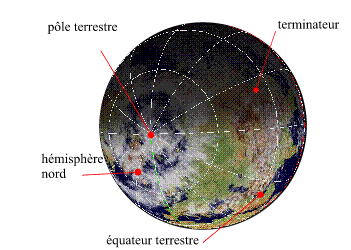
1.4. La durée des jours et des nuits
 |
|
Le jour de l'équinoxe
|
Le jour de l'équinoxe (de printemps ou d'automne),
le terminateur de la zone de nuit sur la Terre passe par les deux pôles
terrestres. Le jour de l'équinoxe, si on néglige la réfraction
atmosphérique, la durée du jour est égale à
la durée de la nuit pour tous les lieux de la surface terrestre.
De plus le jour de l'équinoxe le Soleil se lève exactement
à l'est et se couche exactement à l'ouest.
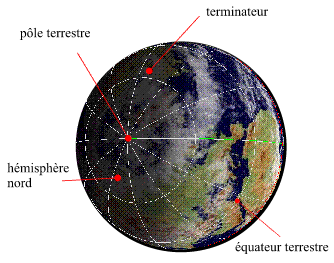 |
|
Le jour du solstice d'hiver
|
Le jour du solstice d'hiver, pour l'hémisphère nord, la demi-sphère
définie par le terminateur de la zone de nuit recouvre la plus grande
partie de la surface de l'hémisphère nord. C'est le jour
de l'année où la durée de la nuit est maximale et
la durée du jour minimale. C'est également le jour où
le Soleil se lève le plus au sud-est, passe au méridien avec
une hauteur minimale et se couche le plus au sud-ouest.
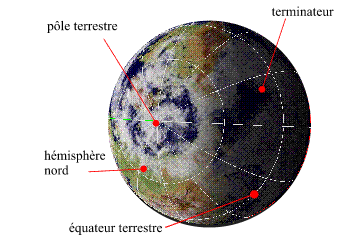 |
|
Le jour du solstice d'été
|
Le jour du solstice d'été, pour l'hémisphère
nord, la demi-sphère définie par le terminateur de la zone
de nuit recouvre la plus petite partie de la surface de l'hémisphère
nord. C'est le jour de l'année où la durée de la nuit
est minimale et la durée du jour maximale. C'est également
le jour où le Soleil se lève le plus au nord-est, passe au
méridien avec une hauteur maximale et se couche le plus au nord-ouest.
La figure suivante illustre les trajectoires apparentes du Soleil pour
chacune de ces journées en un lieu de l'hémisphère
nord.
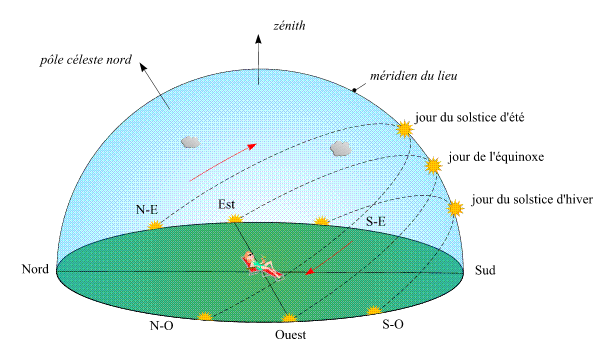
Dans l'hémisphère sud, les solstices et les équinoxes
sont à l'opposé des solstices et des équinoxes de
l'hémisphère nord.
On consultera les pages sur les levers
et couchers des astres pour avoir plus de détails sur la durée
des jours et des nuits.
2. Les dates des saisons
2.1. La révolution tropique
L'intervalle de temps qui sépare deux passages consécutifs
de la Terre dans la direction de l'équinoxe de printemps porte le
nom d'année tropique. Sa valeur moyenne est de 365,2422 jours (soit
365 jours 5h 48m 46s). Cette période est inférieure à
l'année sidérale, qui correspond à l'intervalle de
temps qui sépare deux passages de la Terre dans une même direction
et qui est égale à 365,2566 jours (soit 365 jours 6h 9m 10s).
Ceci est dû au fait que la direction des équinoxes n'est pas
fixe. Elle est animée d'un mouvement de précession dans le
sens rétrograde (50,2877" par an actuellement). Ce mouvement appelé
précession des équinoxes est lié au mouvement de l'axe
de rotation de la Terre qui décrit un cône dans le sens rétrograde
en 26000 ans environ.
2.2. Pourquoi les saisons tombent-elles toujours aux mêmes dates ?
Cela est dû à notre calendrier, le calendrier grégorien,
qui est construit de manière à avoir une longueur moyenne
de l'année la plus proche possible de la révolution tropique
de la Terre. Comme la révolution tropique n'a pas un nombre entier
de jour, si on prend une année calendaire de 365 jours, il y a un
décalage de 0,2422 jour d'une année à l'autre dans
la date des saisons et, au bout de quatre ans, ce décalage est presque
de un jour. Pour compenser ce décalage on a, dans un premier temps,
ajouté un jour à l'année tous les quatre ans (année
bissextile de 366 jours). C'est ce que faisait le calendrier julien élaboré
par Jules César en 46 av. J.-C.
Mais si on ajoute un jour tous les quatre ans, la valeur moyenne de
l'année calendaire est de 365,25 jours. Elle est donc un peu trop
grande par rapport à l'année tropique. Donc si on se contente
d'ajouter une année bissextile tous les quatre ans les saisons vont
se décaler lentement par rapport au calendrier à raison de
0,0078 jour par an (11min 14s par an). Le calendrier julien suit donc mal
les saisons. Il se décale d'environ 3 jours au bout de 400 ans.
Pour avoir une meilleure concordance entre le calendrier et les saisons,
il suffit de supprimer 3 jours sur une période de 400 ans.
C'est ce que l'on fait dans le calendrier grégorien. Comme dans
le calendrier julien, on ajoute une année bissextile tous les quatre
ans (ceux dont le millésime est multiple de quatre) sauf pour les
années qui sont multiples de 100 sans l'être de 400. Ainsi
1600 et 2000 sont bissextiles, mais 1700, 1800, 1900 et 2100 ne sont pas
bissextiles.
Cette réforme du calendrier a été effectuée
par le pape Grégoire XIII en 1582. De plus, pour supprimer le décalage
accumulé entre les saisons et l'ancien calendrier (calendrier julien)
et ramener la date de l'équinoxe de printemps au 21 mars, l'année
1582 a été raccourcie de 10 jours, le lendemain du jeudi
4 octobre 1582 devenant le vendredi 15 octobre 1582.
2.3. Les calendriers utilisés dans le programme de calcul
Le programme de calcul des dates des saisons donne ces dates dans le calendrier
julien pour les dates antérieures au 5 octobre 1582 et dans le calendrier
grégorien pour les dates postérieures au 15 octobre 1582.
Le calendrier julien a été prolongé pour les dates
antérieures au début de l'ère chrétienne. Dans
l'affichage de ces dates on utilise la notation des astronomes et non pas
la notation des historiens.
2.4. La dérive des saisons dans le calendrier julien
Comme nous l'avons vu dans un paragraphe précédent, les dates
des saisons se décalent dans le calendrier julien d'environ 3 jours
tous les 400 ans. On peut constater cette dérive à l'aide
du programme de calcul des saisons.
| Année |
Printemps |
Eté |
Automne |
Hiver |
| 0 |
22 mars |
24 juin |
25 septembre |
22 décembre |
| -1000 |
30mars |
2 juillet |
2 octobre |
29 décembre |
| -2000 |
7 avril |
10 juillet |
9 octobre |
6 janvier |
| -3000 |
14 avril |
18 juillet |
15 octobre |
13 janvier |
| -4000 |
22 avril |
25 juillet |
22 octobre |
20 janvier |
Dérive de la date des saisons dans le calendrier julien
2.5. Les dates des saisons dans le calendrier grégorien
Nous l'avons vu, le calendrier grégorien est conçu pour éviter
le décalage des dates des saisons que nous avons constaté
dans le calendrier julien. Les dates des saisons restent donc toujours
au voisinage des mêmes dates dans le calendrier grégorien.
L'utilisation des années bissextiles fait osciller l'instant des
saisons sur trois et, exceptionnellement, quatre jours.
Les dates de l'équinoxe de printemps
Aux XIXème et XXème siècles,
l'équinoxe de printemps tombe toujours le 20 ou le 21 mars. Dans
le passé il est tombé le 19 mars en 1652, 1656, 1660, 1664,
1668, 1672, 1676, 1680, 1684, 1685, 1688, 1689, 1692, 1693, 1696, 1697,
1780, 1784, 1788, 1792 et 1796.
Il tombera de nouveau le 19 mars en 2044.
Les dates du solstice d'été
Dans le calendrier grégorien, le solstice d'été peut
tomber les 19, 20, 21 ou 22 juin. En général, il tombe le
21 juin. Il est tombé un 20 juin en 1896 et tombera de nouveau à
cette date en 2008. Il est tombé un 22 juin en 1975 et tombera de
nouveau à cette date en 2203, 2207, 2211 et 2215 puis en 2302. Le
solstice d'été tombera un 19 juin en 2488 (et ce sera la
première fois depuis la création du calendrier grégorien)
puis en 2492 et 2496.
Les dates de l'équinoxe d'automne
Dans le calendrier grégorien, l'équinoxe d'automne peut tomber
le 21, 22, 23 ou 24 septembre. Il tombe en général le 22
ou le 23 septembre. Il tombera le 21 septembre en 2092 et ce sera la première
fois depuis la création du calendrier grégorien. Cela se
reproduira en 2096, puis en 2464, 2468, 2472, 2476, 2480, 2484, 2488, 2492,
2493, 2496 et 2497. Il est tombé un 24 septembre en 1803, 1807,
1903, 1907, 1911, 1915, 1919, 1923, 1927 et 1931, il tombera de nouveau
à cette date en 2303.
Les dates du solstice d'hiver
Dans le calendrier grégorien le solstice d'hiver peut tomber le
20, 21, 22 ou 23 décembre. Il tombe en général le
21 ou le 22 décembre. Il est tombé un 23 décembre
en 1903 et tombera de nouveau à cette date en 2303, 2307, 2311 et
2315. Il est tombé un 20 décembre en 1664, 1668, 1672, 1676,
1680, 1684, 1688, 1692, 1696 et 1697 et tombera de nouveau à cette
date en 2080, 2084, 2088, 2092, 2096, 2488, 2492 et 2496.
3. La durée des différentes saisons
3.1. La longueur des saisons
Il suffit de consulter un calendrier pour vérifier que les longueurs
des différentes saisons ne sont pas égales. Par exemple durant
l'année 1998, l'hiver a duré 89 jours, le printemps 92 jours
18 heures, l'été 93 jours 15 heures et l'automne 89 jours
21 heures.
Cette variation des longueurs des saisons provient du fait que la vitesse
du barycentre Terre-Lune sur son orbite autour du Soleil n'est pas un mouvement
uniforme. C'est une conséquence immédiate de la seconde loi
de Kepler. La vitesse orbitale n'est pas constante. Donc lorsque le barycentre
Terre-Lune est au plus près du Soleil (à son périhélie)
sa vitesse est maximale et lorsque le barycentre Terre-Lune est au plus
loin du Soleil (à son aphélie) sa vitesse est minimale. Or
actuellement le barycentre Terre-Lune passe au périhélie
début janvier et à l'aphélie début juillet.
Donc la Terre est plus rapide sur son orbite en janvier et l'hiver est
la saison la plus courte, de même elle est la plus lente en juillet
et l'été est la saison la plus longue.
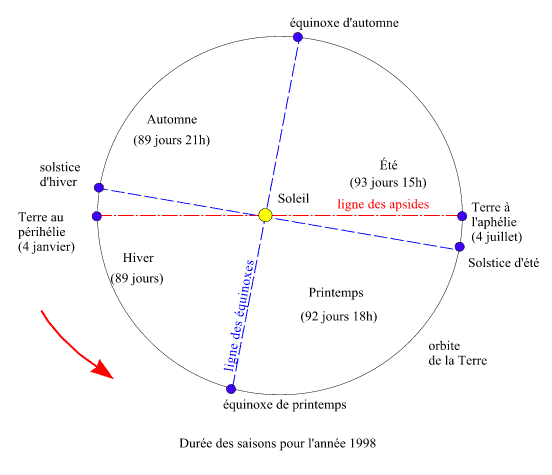
Cette figure montre bien que la saison n'est pas fonction de la distance
entre le Soleil et la Terre. Actuellement, dans l'hémisphère
nord, la saison la plus froide (l'hiver) correspond à l'époque
où le Soleil est le plus près de la Terre et la saison la
plus chaude (l'été) correspond à l'époque où
le Soleil est le plus loin de la Terre.
3.2. L'évolution de la longueur des saisons
Si les positions du périhélie et de l'aphélie du barycentre
Terre-Lune étaient constantes dans le temps, la durée des
différentes saisons serait, elle aussi, constante. Mais l'orbite
du barycentre Terre-Lune tourne dans son plan dans le sens direct à
raison d'environ 12" par an (soit une révolution en environ 100000
ans). La précession des équinoxes s'effectue dans le sens
contraire (sens rétrograde) à raison de 50,2877" par an (soit
une révolution en environ 26000 ans). La combinaison de ces deux
mouvements permet de calculer la période du passage du périhélie
de la Terre par la direction de l'équinoxe de printemps, cette période
d'environ 21 000 ans est appelée précession climatique. En
effet, tous les 10500 ans (demi-période de la précession
climatique) l'aphélie passe de l'été à l'hiver.
Or même si la distance Terre-Soleil n'est pas le facteur prédominant
dans la nature des saisons, la combinaison du passage de la Terre à
l'aphélie en hiver donne des hivers plus rudes.
4. Un peu d'histoire
4.1. La précession des équinoxes et la longueur de l'année
tropique
Le nom d'Hipparque de Nicée (env. 190 - env. 125 av. J.-C.) est
lié à la découverte de la précession des équinoxes.
Pour découvrir ce lent mouvement de la ligne des équinoxes,
deux méthodes d'observation sont possibles. La première consiste
à mesurer les variations des longitudes des étoiles au cours
du temps. Cette méthode est cumulative, car chaque année
la longitude croît d'une valeur faible mais constante. La deuxième
méthode consiste à mesurer l'écart entre l'année
tropique et l'année sidérale. Nous savons grâce à
Ptolémée (IIème siècle après J.-C.)
qu'Hipparque a utilisé ces deux méthodes. Et c'est vraisemblablement
la première qui fut à l'origine de sa découverte de
la précession des équinoxes. Pour cela il compara la distance
de Spica dans l'Épi de la Vierge (l'étoile alpha Virginis)
avec l'équinoxe d'automne aux dates des observations de Timocharis,
observations faites entre 294 et 283 av. J.-C. et la valeur de cette même
distance à son époque, et il trouva une variation dans la
longitude de l'étoile de 2° sur la période de 160 ans
séparant les deux mesures.
Pour la détermination des valeurs de l'année tropique
et de l'année sidérale, Hipparque utilisa dans un premier
temps des observations faites entre 162 et 128 av. J.-C., mais les valeurs
calculées à partir de ces observations semblaient indiquer
une valeur variable de l'année tropique en fonction du temps. Finalement,
il se limita aux observations des solstices qu'il avait effectuées
lui-même en 135 av. J.-C., aux observations faites par Aristarque
en 280 av. J.-C. et aux observations faites par Méton, en 432 av.
J.-C. Pour l'année tropique il trouva une valeur de 365 jours 1/4
moins 1/300 jour (soit 365 jours 5h 55m 12s) et pour l'année sidérale,
il trouva une valeur de 365 jours 1/4 plus 1/144 jour (soit 365 jours 6h
10m 0s). Ces valeurs sont assez proches des valeurs actuelles.
Le tableau suivant donne les différentes valeurs de l'année
tropique en fonction de l'époque.
| Epoque |
Auteur |
Valeur |
| 141-127 av. J.-C. |
Hipparque |
365j 5h 55m 12s |
| 45 av. J.-C. |
Jules César (Sosigène) |
365j 5h 55m |
| 139 ap J. C. |
Ptolémée |
365j 5h 55m 12s |
| 499 |
Aryabhata |
365j 8h 36m 30s |
| 882 |
al-Battani |
365j 5h 48m 24s |
| ~1100 |
Khayam |
365j 5h 49m 12s |
| 1252 |
Tables Alphonsines |
365j 5h 49m 16s |
| ~1440 |
Ulug Beg |
365j 5h 49m 15s |
| 1543 |
Copernic |
365j 5h 49m 29s |
| 1574-1575 |
Danti |
365j 48m |
| 1582 |
Calendrier Grégorien |
365j 48m 20s |
| 1986 |
Laskar |
365j 5h 48m 45.187s |
En réalité la valeur de l'année
tropique n'est pas constante, mais varie lentement en fonction du temps,
sa valeur est donnée pour un instant donné par la relation
suivante (J. Laskar, 1986) :
A =3 65,242 189 669 8 - 0,000 006 153 59 T - 7,29 x 10 -10
T 2 + 2,64 x 10 -10 T 3
où T = (JJD - 2 451 545,0) / 36 525
JJD étant le jour julien de l'époque considérée.
4.2. La longueur des saisons
Le Papyrus d'Eudoxe, nous informe que Callipe (vers 370-330 av. J.-C.)
fut un des premiers astronomes à déterminer avec précision
la longueur des différentes saisons. Il trouva (94, 92, 89 et 90
jours) à partir de l'équinoxe de printemps. Hipparque améliora
ces valeurs et trouva (94 1/2, 92 1/2, 88 1/8 et 90 1/8) toujours à
partir de l'équinoxe de printemps. On remarquera que ces valeurs
sont très différentes des valeurs actuelles et cela est normal.
En effet, si l'on tient compte de la précession climatique, l'angle
entre le périhélie et l'équinoxe de printemps était
à l'époque d'Hipparque 34° plus grand qu'actuellement.
Le périhélie tombait donc en automne et l'aphélie
au printemps, et la saison la plus courte était effectivement l'automne
et la saison la plus longue, le printemps. |
 Comprendre - Concepts fondamentaux - Saisons
Comprendre - Concepts fondamentaux - Saisons Comprendre - Concepts fondamentaux - Saisons
Comprendre - Concepts fondamentaux - Saisons

